记录一下硕士课题做的东西,方便翻旧账
高空建筑机器人实现末端轨迹跟踪任务
本课题拟实现一款多用途的、智能的、可靠的高空建筑机器人,在不接触墙体的前提下,控制机器人在高空完成喷漆、划线等任务。
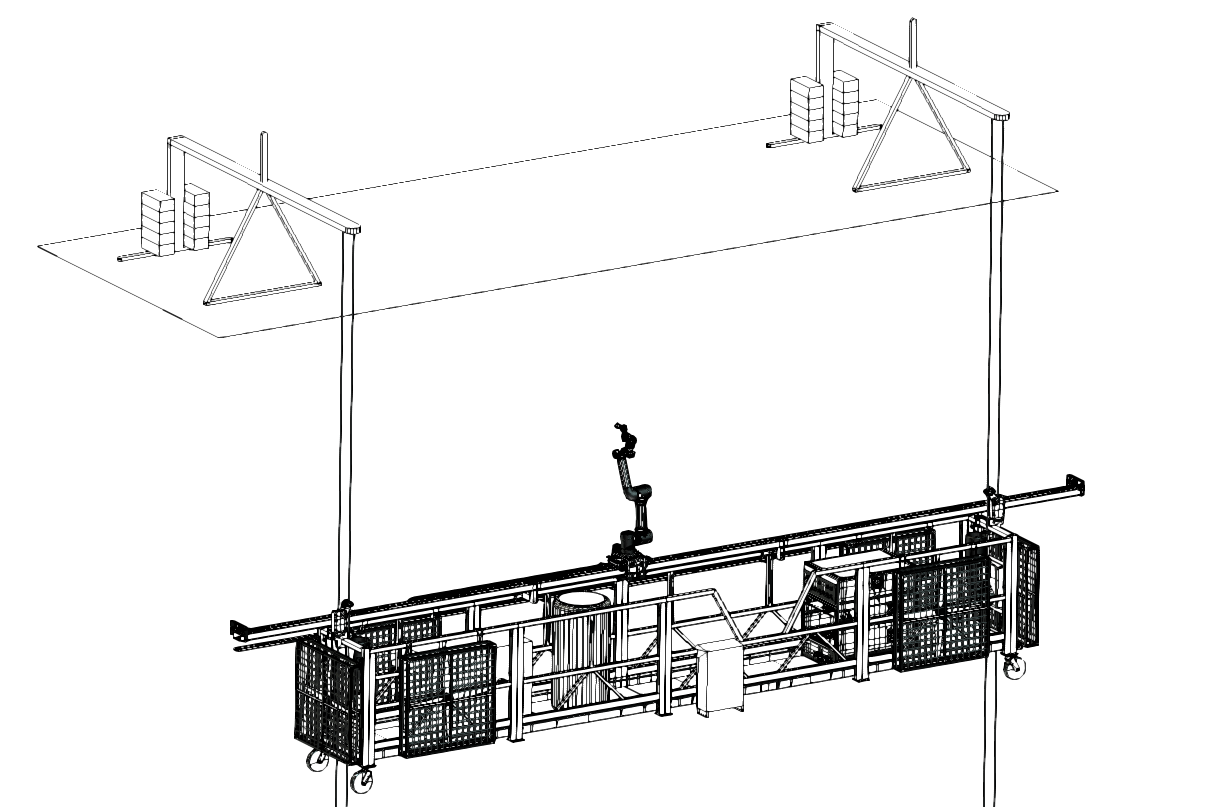
非接触式高空建筑机器人本质是一个欠驱动系统,因为绳吊式施工方法,我们不能通过给钢绳施加力或力矩实现吊篮基座的位姿控制。在高空基座容易受到高楼横风的影响,同时当机械臂和导轨工作时的反作用也会使基座晃动起来。确保工作环境下平台的稳定是实现室外高空自动化施工的前提条件,必须优先攻克这一关键技术问题。在执行喷漆、画线等施工任务时,保证机械臂末端跟踪任务轨迹是本课题控制问题的关键。由于平台自身存在晃动,以及该机器人系统运动的强耦合性,机械臂末端轨迹跟踪任务变得较为困难。
具体地,本课题主要集中于机器人的运动控制,以及运动规划。围绕这一目标的实现,在技术上本课题将开展以下研究内容:
(1)室外高空建筑机器人系统动力学建模
(2)室外高空建筑机器人摆动平台稳定;
(3)室外高空建筑机器人末端轨迹跟踪实现;
1、非墙面接触式高空建筑机器人存在被动关节,为欠驱动系统
2、机器人吊篮的自由度建模,运动学,动力学建模
3、欠驱动系统控制仍为一个开放性问题,暂时缺少普遍实用的方法
通过分析吊篮的运动,我们可以知道吊篮具有四个自由度,本课题将其定于为以下四个独立的广义坐标:
- 绕上方悬吊点两个方向(图中Z1和Z2)的转动(广义自由度1 q和2 q)产生的仅仅位置变化
- 围绕下方悬吊点两个方向(图中Z3和Z4)的转动(广义自由度3 q和4 q)产生的仅仅姿态变化
即1 q 2 q与3 q 4 q是解耦的
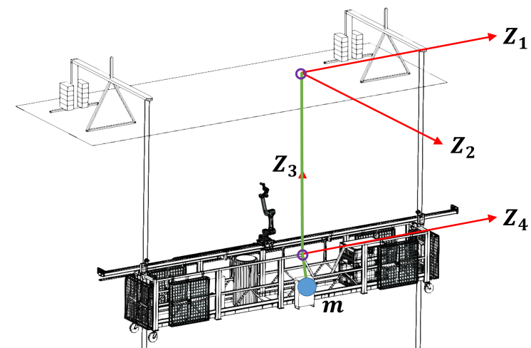

由此,吊篮连体坐标系∑0在惯性坐标系∑I下的齐次变换矩阵为:
T0I=⎣⎢⎢⎢⎡cos(q3)cos(q4)sin(q3)cos(q4)−sin(q4)0−sin(q3)cos(q3)00cos(q3)sin(q4)sin(q3)sin(q4)cos(q4)0lsin(q1)cos(q2)lsin(q2)lcos(q1)cos(q2)1⎦⎥⎥⎥⎤
接着,采用D-H法建立导轨加上六轴机械臂共七自由度的运动学模型,得到其D-H参数表。由D-H参数表便可求得机械臂末端坐标系到吊篮坐标系坐标系 的齐次变换矩阵,进而得到机械臂末端坐标系在惯性坐标系∑0下的位姿。
对于具有多变量、强耦合特点的欠驱动机器人系统,相对传统牛顿力学方法,欧拉-拉格朗日(Euler-Lagrange)法通过能量的计算,更方便推导欠驱动系统的动力学模型。
前面我们已经定义吊篮的四个广义自由度,以及机器人系统上七个可驱动自由度,我们可以利用欧拉-拉格朗日法计算机器人的动力学方程。
因为我们对吊篮广义自由度的建模设定,需要对钢丝拉力在q3上的分力矩进行建模。我们知道,当吊篮发生沿垂直方向扭转时,它会往复摆动,这是由于绳子拉力造成的。我们还需要建立绳子拉力在这个转动自由度上的分力模型。
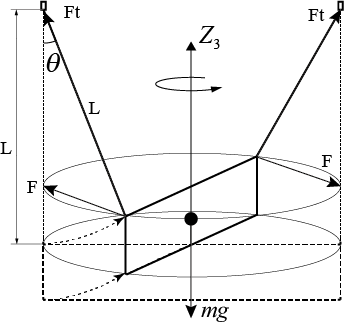
我们假设绳长不变,此时绳子拉力在吊篮上的作用点位于以绳长为半径的球面上;同时,假设吊篮扭转时,吊篮垂直转轴Z3位于吊篮俯视图(图2-4)中心,且固定位置不变,此时绳子拉力在吊篮上的作用点位于以垂直转轴为中心,吊篮长为直径的圆柱面上。基于上面两个假设,绳子拉力作用点为球面与圆柱面交线上,随着转角增加,在垂直方向上上移,即吊篮高度随着转角会向上小幅移动,如图2-5所示。这是符合实际的,吊篮在垂直方向往复转动,实际就是重力势能和动能不断转换的结果。
此时,重力和绳子拉力在水平面的分力为:
F=2mgtanθ
其中,
tanθ≈θ=2Lq3R
水平面的分力对转轴的力矩为:
τ=2RF⋅sin(2π−2q3)
由于有两根钢丝绳,故可以得到广义自由度q3上的广义力为:
τ3=2τ=4L−mgR2⋅q3⋅cos(2q3)
其中,m为机器人的总质量,g为重力加速度,R为吊篮上两悬吊点之间的距离,L为钢丝绳长。

设吊篮被动广义坐标为qp∈R4×1,可驱动关节广义坐标为qa∈R7×1,则系统可写成分块形式:
Mpp(q)q¨p+Map(q)q¨a+Cp(q,q˙)=0Map(q)q¨p+Maa(q)q¨a+Ca(q,q˙)=τa
其中,τa∈R7×1为机器人可驱动关节。




